1-есеп
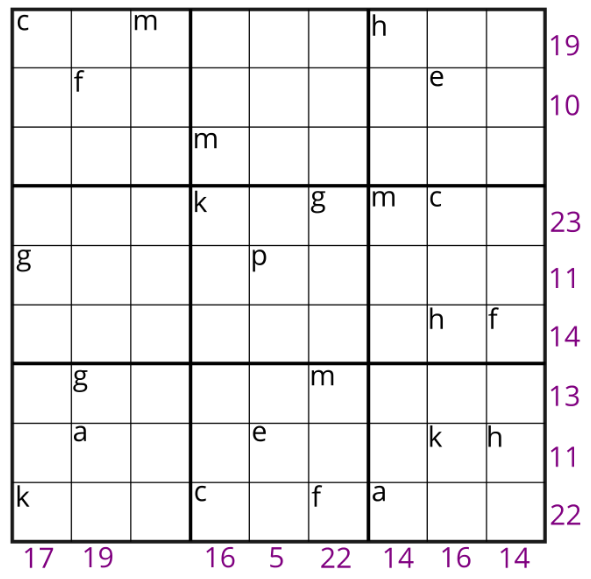
Судокуды шешу екі қадамнан тұрады:
1) Әр бағанда, әр жолда және әр $ 3\times3 $ шаршыда 1-ден 9-ға дейінгі сандар болуы керек.
2) Ешқандай баған, жол немесе әр $ 3\times3 $ шаршыда бірдей санмен екі шаршы болмайды.
Біреу жоғарыдағы судоку жұмбағындағы 1-ден 9-ға дейінгі әр санды әріппен алмастырды. Жолдың немесе бағанның төменгі жағындағы сан сол жолда немесе бағанда көрсетілген әріптердің қосындысы екенін ескере отырып, қай әріп қай санға сәйкес келетінін тауып, судокуды шешуге болады ма?
Барлығы 16 теңдеулер жиынтығын құруға болады
Мысалы, $ 9\times9 $ тордың сол жағынан басталатын бірінші және екінші бағандардан келесі теңдеулерді құрастыруға болады:
$c+g+k=17$
$f+g+a=19$
$ 9\times9 $ тордың жоғарғы жағынан басталатын төртінші және бесінші қатарлардан келесі теңдеулерді алуға болады:
$k+g+m+c=23$
$g+p=11$
2-есеп
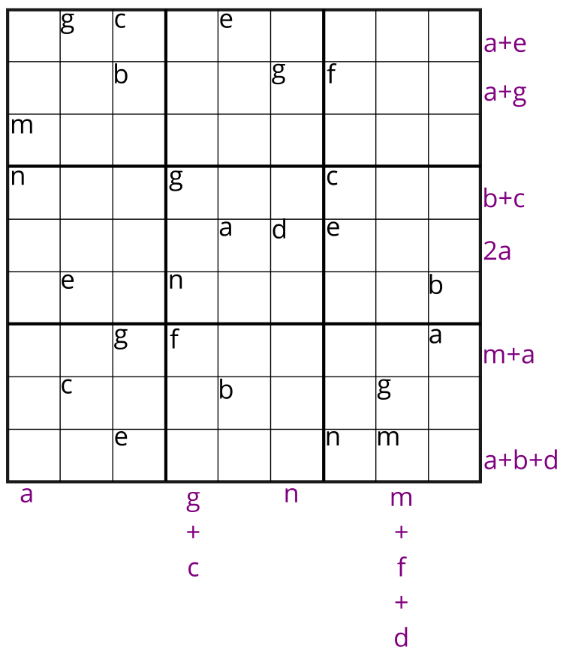
Енді жолдар мен бағандардың соңындағы сандар да әріптермен алмастырылды. Он теңдеуді шешіп, содан кейін cудокуды шеше аласыз ба?
Мысалы, $ 9\times9 $ шаршының сол жағынан басталатын бірінші және төртінші бағандардан келесі теңдеулерді құруға болады:
$m+n=a,$
$g+n+f=g+c.$
$m+n=a,$
$ 9\times9 $ шаршының жоғарғы жағынан басталатын екінші және соңғы жолдардан келесі теңдеулерді құруға болады:
$b+g+f=a+g,$
$e+n+m=a+b+d.$
1-есеп
1. Барлық теңдеулерді жазып алыңыз. Қарапайым көрінетін теңдеулер қайсысы? Егер сізде тек екі әріптен тұратын теңдеу болса, әр әріптің 1 мен 9 арасындағы әр түрлі сан екенін біле отырып, сол әріптердің мүмкін болатын мәндерін жазып бере аласыз ба?
2. Сандардың бір ғана мүмкін комбинациясы бар кез-келген теңдеуді байқай аласыз ба? Мысалы, егер $a+b+c+d=10,$ мұндағы $ a,b,c $ және $ d — $ 1 мен 9 аралығындағы бүтін сандар болса, онда мүмкін болатын сандар $ 1+2+3+4=10 $ болады. Мұны әр әріп үшін мүмкін мәндерді кішірейту үшін қолдана аласыз ба?
2-есеп
Барлық теңдеулерді жазып, мүмкіндігінше жеңілдетіңіз. Бірдей әріптері бар теңдеулерді анықтаңыз. Жұмбақты шешу үшін 1-есепте қолданған әдісіңізді қолданып көріңіз
1-есеп
Сонымен берілген теңдеулер мыналар:
(1) $ c+m+h=19$
(2) $ c+m+h=19$
(3) $ k+g+m+c=23$
(4) $ g+p=11$
(5) $ h+f=14$
(6) $ g+m=13$
(7) $ a+e+k+h=11$
(8) $ k+c+f+a=22$
(9) $ c+g+k=17$
(10) $ f+g+a=19$
(11) $ m+k+c=16$
(12) $ p+e=5$
(13) $ g+m+f=22$
(14) $ h+m+a=14$
(15) $ e+c+h+k=16$
(16) $ f+h=14$
Алдымен ең қарапайым екі белгісіз теңдеулерді қарастырайық.
$g+m=13$
$g+m+f=22$
Бұл екі теңдеуден f-тің мәні 9-ға тең екендігін көруге болады. осылайша табылған сандарды теңдеулерге қоя отырып барлық сандарды табамыз:
| Әріп | Мәні |
|---|---|
| a | 3 |
| c | 8 |
| e | 1 |
| f | 9 |
| g | 7 |
| h | 5 |
| k | 2 |
| m | 6 |
| p | 4 |
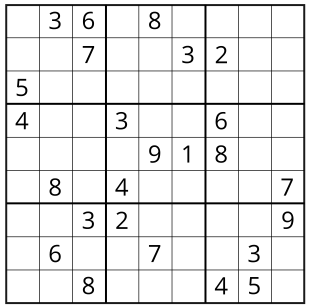
Сонымен біз мынадай судокуды аламыз:
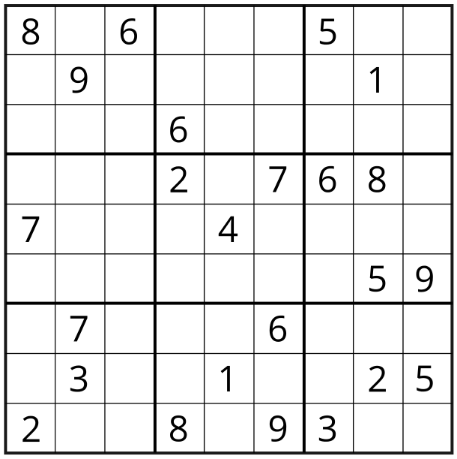
Судокудың жауабы:
2-есеп
Бұл судокудан 10 теңдеу алуға болады:
(1) $ m+n=a$
(2) $ g+n+f=g+c \Rightarrow n+f=c$
(3) $ g+d=n$
(4) $ g+m=m+f+d \Rightarrow g=f+d$
(5) $ g+c+e=a+e \Rightarrow g+c=a$
(6) $ b+g+f=a+g \Rightarrow b+f=a$
(7) $ n+g+c=b+c \Rightarrow n+g=b$
(8) $ a+d+e=2a \Rightarrow d+e=a$
(9) $ g+f+a=m+a \Rightarrow g+f=m$
(10) $ e+n+m=a+b+d$
3 пен 4-ші теңдеулерден g -ді жойып жіберіп, мынаны аламыз:
$f+d=n−d \Rightarrow n=2d+f$
$n=c−f$ 2-ші теңдеуінен
$c−f=2d+f \Rightarrow c=2d+2f$
өрнектеп аламыз.
Осы теңдеуден біз с жұп екенін көреміз, сондықтан $c=6$ болса, d мен f — 1 мен 2-ге тең, немесе $c=8$ болса d мен f — 1 мен 3-ке тең.
$g+c=a$ 5-ші теңдеуін қарастырайық, егер $c=6$ болса, онда g-дің ең үлкен мәні 3-ке тең. d мен f-тің екеуінің біреуі 1-ге тең болғандықтан және $a\leq 9 $ болғандықтан
$c=6$
Онда d мен f мәндері 1 мен 2-нің біреуіне тең, демек
$g=3$
5-теңдеуді қарастырсақ,
$a=9$
екендігі шығады.
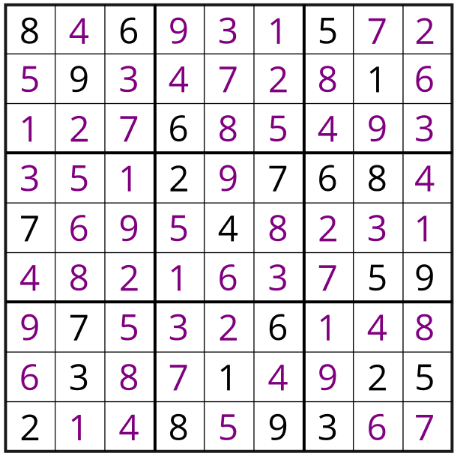
Осылайша барлық элементтерді тауып шығамыз:
| Әріп | Мәні |
|---|---|
| a | 9 |
| b | 7 |
| c | 6 |
| d | 1 |
| e | 8 |
| f | 2 |
| g | 3 |
| m | 5 |
| n | 4 |
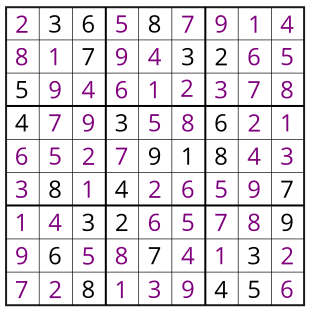
Табылған мәндерді алмастырып шығайық:
Судокудың шешімі:
Жазба сіз үшін қаншалықты қажет болды?
Жұлдызшаның үстінен басыңыз!
Бұл жазбаның сіз үшін қажетті болмағаны өкінішті!
Жазбамызды жақсартайық!
Жазбаны жақсартуға қандай ұсыныс айтар едіңіз?